Người ta tính được các chỉ tiêu về sản xuất của công ty Nimbus, giống kết quả bài 17, như được thể hiện lại dưới đây:
Yêu cầu:
1. Dựa vào cột sản lượng và cột tổng chi phí (chỉ cần cột nền vàng), hãy ước lượng hàm tổng chi phí TC=f(Q) theo dạng hàm đa thức bậc hai, với tung độ góc đúng bằng chi phí cố định là 200. Kết quả trên nói lên được điều gì?
2. Tính các chỉ tiêu chi phí gồm: TC, TFC, TVC, ATC, AFC, ACV và MC tại mức sản lượng Q=100
BÀI GIẢI
Câu 1:
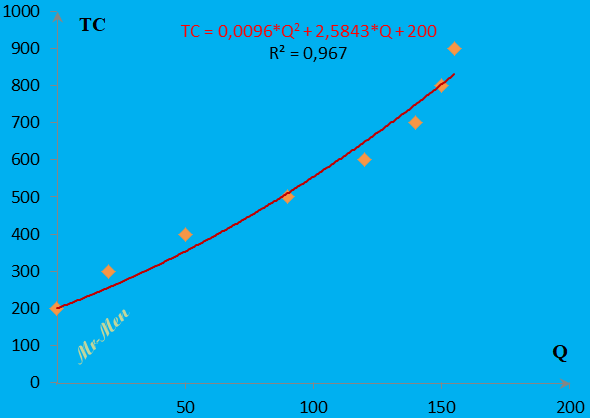Từ hai cột số liệu trên, sử dụng công cụ đồ thị Scatter và những lựa chọn khi Add trendline (nhấp chuột phải), kết quả có được mô hình ước lượng như hình bên.
Hàm số TC = 0,0096*Q2 + 2,5843*Q + 200 thể hiện chi phí tăng tốc độ càng nhanh khi sản lượng càng lớn. Điều này phản ánh một quy luật cần lưu ý trong sản xuất, đó là tổng chi phí sẽ tăng nhanh khi tăng sản lượng. Quy luật này cũng dễ hiểu và luôn tồn tại trong thực tế. Dữ liệu bài này và dữ liệu ban đầu từ bài 17 đều thể hiện việc tăng nhanh chi phí là do quy luật năng suất biên giảm dần, khi sử dụng nhiều lao động làm việc trong điều kiện chật chội, thiếu công cụ dụng cụ. Trong thực tế, việc khan hiếm các yếu tố đầu vào như nguyên vật liệu cũng có thể sẽ làm tổng chi phí tăng nhanh khi tăng sản lượng.
Câu 2:
Một khi có hàm số TC = 0,0096*Q2 + 2,5843*Q + 200, việc xác định 7 đại lượng chi phí trở nên đơn giản, chỉ bằng việc thế Q=100 vào phương trình.
Tại Q = 100,
Tổng chi phí cố định: TFC = 200 (không đổi)
Tổng chi phí biến đổi: TVC = 0,0096*1002 + 2,5843*100 = 354,4
Tổng chi phí : TC = TFC+TVC = 200 + 354,4 = 554,4
Định phí trung bình: AFC = TFC/Q = 200/100 = 2
Biến phí trung bình: AVC = TVC/Q = 354,4/100 =3,54
Tổng chi phí trung bình: ATC = AFC+AVC = 2 + 3,54 = 5,54
Chi phí biên: MC = TC’ = 2*0,0096*100+2,5843 = 4,50 (MC là đạo hàm của TC).
